|

horizontal
tail: pitch, stability and
control
By Chris Heintz
Stability: A system is stable
when it comes back to its original state after it was submitted to an
external disturbance. The classic example is a ball in a bowl (see Figure 1). In
an unstable system, a disturbance will produce an ever-increasing change
from the original state; the corresponding classic example is a ball on a
hilltop (see Figure 2). The new state is at rest but different from the
original. Example: A ball on the pool table (see Figure 3).
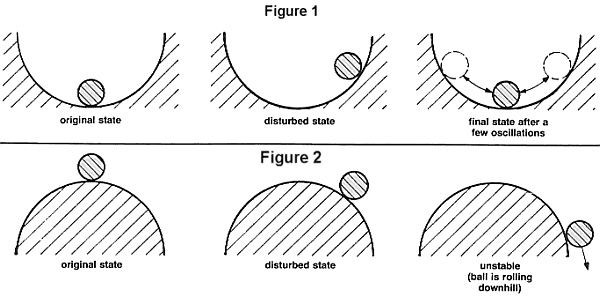
Indifferent stability is the
boundary between stable and unstable. This is easily imagined when we see the
ball in the bowl. Then visualize the bowl opening more and more, becoming a flat
surface and then the original inside becoming the outside of the bowl (see
Figure 4). When applied to an aircraft, the concept of stability means: At a
given power setting, the aircraft has been trimmed to a certain speed when the
pitch control is left untouched. If a disturbance occurs (a gust or a short push
or pull on the control), the aircraft is said to be stable if it returns to its
original speed (this is associated to the aircraft's nose position with respect
to the horizon). It is said to be unstable if the disturbance produces an
ever-increasing amplitude of the speed until the aircraft hits the ground or
stalls. It is said to be indifferent if the speed stabilizes at a different
value than the original trim speed.
Most of the time and in all three cases there are usually
several oscillations. The oscillations have usually a short period (say less
than five seconds). For the pilot, what does it mean if his aircraft is not
stable?. All that is required is to take hold of the pitch control and bring the
speed back to the trim speed. This is obviously not a dangerous situation,
although it may be quite tiring on a long cross-country flight if the aircraft
does not fly "hands off." We simply have to "fly it" all the time. Note the
above applies to VFR flying; an IFR unstable aircraft is dangerous because the
pilot's workload becomes too much when we have to concentrate on the instruments
as well as keeping the speed steady.
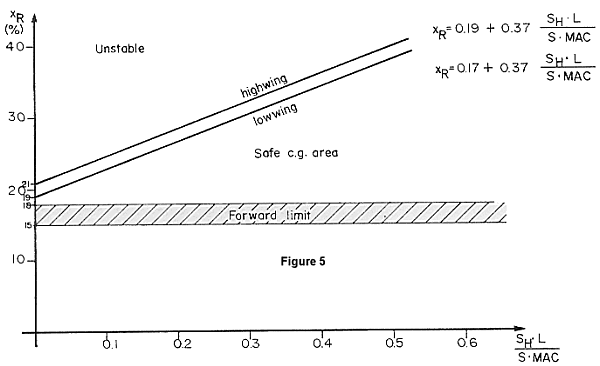
From a design standpoint, the graph (see Figure 5) allows us to
design a stable aircraft. XR is the most rearward
position of the centre of gravity where the aircraft is still stable. If
X, which is the actual centre of gravity position, is smaller than
XR, the aircraft is stable and can be flown hands
off.
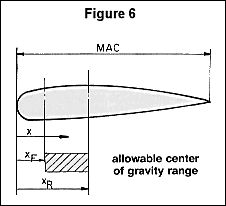
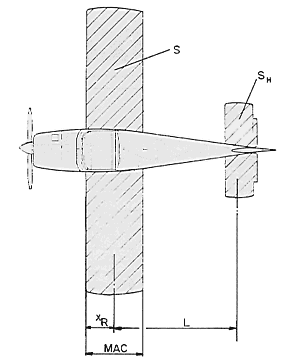
Because an aircraft flies mainly with its wing, the wing
leading edge is the reference for measuring X and
XR (see Figure 6). The two lines in the diagram
represent the following formula:
XR = .17 + .37
SH/S x L/MAC - Low Wing
XR = .19 + .37
SH/S x L/MAC - High Wing
where:
SH horizontal tail
area
S wing area
L distance from DR to horizontal
tail centre of lift
MAC wing mean aerodynamic chord
(SH x L is sometimes called
horizontal tail volume because it is the tail surface times another
dimension.)
Because L is a function of XR,
a trial and error process is necessary to solve the equation. We will not go
into those details as it is quite all right to measure L from the wings'
centre of lift to the horizontal tail's centre of lift, which are both very
close to the quarter chord point.
The formula takes into account that a high wing aircraft, due
to the pendulum effect, is slightly more stable than a low wing aircraft, all
other factors being the same.
It is also interesting to know that the formula applies to
classic as well as canard aircraft and even to flying wings (tailless aircraft),
although both L and SH are equal to
zero.
To my knowledge, it has no theoretic foundation, it is based
strictly on statistics and is surprisingly accurate. I would be interested to
hear from a stability specialist when he has discovered the theory behind
it.
|
